Merkle Tree
Overview of Merkle Tree, membership proofs, and consistency proofs
About Merkle Tree
A Merkle Tree is a tree structure where each leaf node is a cryptographic hash of its underlying data and each non-leaf node is a hash of its direct descendants. Typically, Merkle trees have a branching factor of two, meaning that each node has up to two children. At the top of each tree is the root hash which changes each time a new leaf node is added to the tree.
Below is an example of a simple Merkle Tree with two leaf nodes. HA and HB are hashes of A and B respectively. Their parent, also the root hash, is a hash of each child H(HA,HB) represented as HAB.
Understand membership proof
A membership proof, also known as a Merkle Proof, is a set of hashes that can be used to prove a given leaf's membership in the tree. A proof is given for a specific leaf node and is comprised of the leaf's sibling, and each non-leaf hash that could not otherwise be calculated without additional leaf nodes. To prove membership the two siblings are hashed to create a parent hash and then repeatedly combined with each hash in the proof to calculate a root hash. The calculated root hash can be compared with the known root hash to see if they match. Matching hashes prove that the provided leaf node is a member of the tree.
Expanding on the earlier example, two more leave nodes are added to the tree.
To prove C's membership in the tree a Merkle Proof can be provided. To do this, the hash of C is calculated and the hashes HD and HAB are provided - this is the Merkle Proof. Using these hashes a root Hash can be calculated and then compared to the current root hash. If the root hash matches then C's membership is proven.
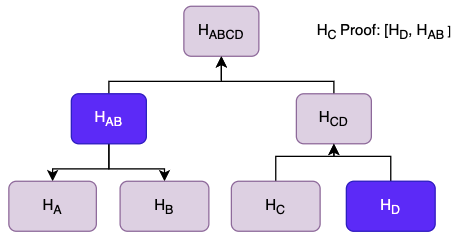
To calculate the root hash:
HCD = H(HC, HD)
Hroot = HABCD = H(HAB, HCD)
Outline consistency proof
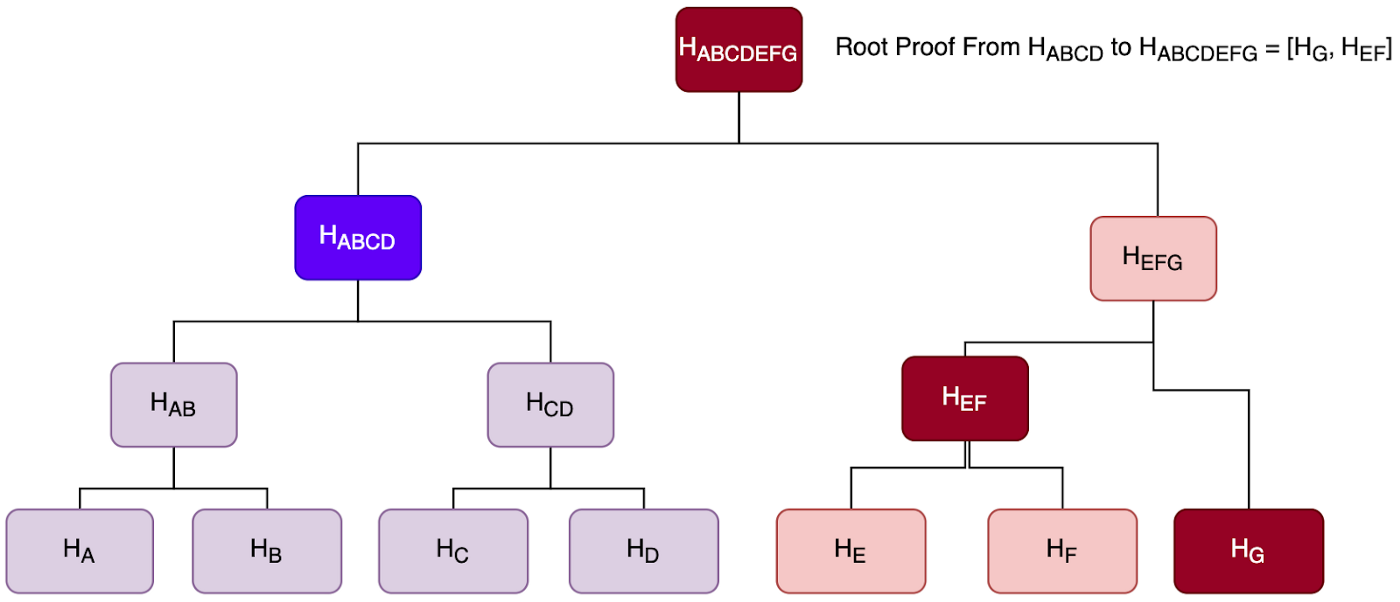
A consistency proof is a set of hashes that can be used to prove that a current root hash is a continuation of a previous root hash. The consistency proof consists of the root hash of each newly completed subtree since the previous root hash was created. Then, just like the membership proof, the current root can be calculated.
Was this article helpful?